Hands-On: Mixed Integer Linear Programming für Last-Mile Delivery

Bei der Lieferung von Arzneimitteln auf dem „letzten Kilometer“ zum Anwender (engl.: Last-Mile) geht es um den Transport von Medikamenten und medizinischen Geräten von einem zentralen Lager zu Apotheken, Kliniken, Krankenhäusern und anderen Einrichtungen. Dieser Prozess muss äußerst zuverlässig und effizient sein, um auf unvorhergesehene Notfälle und Nachfragen reagieren zu können.

Was, wenn Drohnen die Notfallversorgung schneller und in schwer erreichbaren Gebieten ermöglichen?

Durch die drohnen-gestützte Anlieferung eines Defibrillators an einen Patienten mit Herzstillstand in Schweden konnten beispielsweise erste Schocks verabreicht werden, bevor die Rettungssanitäter eintrafen. Ein anderes aktuelles Beispiel ist die Verteilung von Blutkonserven per Drohne in Großstädten und im ländlichen Raum. Schneller Zugang zu lebensrettender Ausrüstung ist essenziell bei der medizinischen Notversorgung. Eine optimierte Routenführung führt zu einer effizienten Nutzung der verfügbaren Ressourcen.

Wie hilft gemischt-ganzzahlige Optimierung bei der Logistik?

Bei der Logistik werden regelmäßig gemischt-ganzzahlige Optimierungsprobleme (wie CVRP) gelöst, um effiziente Transportwege zu finden. Diese Probleme gehören zum Bereich des Operations Research. Dabei geht es um die Optimierung der Nutzlast für jedes Fahrzeug und die Bestimmung der kürzesten Routen mit mehreren Lieferadressen. Ziel ist es, die Abläufe mit optimalen Auslieferungszeiten zu finden.

Dafür vereint man zwei bekannte ganzzahlige lineare Optimierungsprobleme:

• Nutzlastkapazität (Knapsack-Problem)
• Zeitliche Beschränkungen (Traveling Salesman Problem)

Der Algorithmus optimiert die Nutzlast und die Lieferreihenfolge, um eine effiziente und koordinierte Zustellung der Pakete sicherzustellen. Dafür wird die sogenannte MILP Modellierung herangezogen.

Dieses Tutorial soll Logistikern, OR-Analysten und Unternehmensberatern bei der Anwendung von Quantagonia’s HybridSolver helfen.

How to: Implementierung von Mixed Integer Linear Programming in Python

Das Aufsetzen eines Optimierungsproblems in Python folgt einer strukturierten Herangehensweise.

1. Definition der relevanten Parameter (z.B. Lieferorte)
2. Definition der Zielfunktion (z.B. Minimierung der Gesamtentfernung)
3. Definition der Nebenbedingungen (z.B. Fahrzeugkapazität)
4. Modell berechnen / optimieren
5. Verarbeitung der Resultate

Diese Struktur sorgt für Klarheit und macht es einfacher, den Code zu verstehen und später zu ändern.

Beispiel Code-Implementierung: Optimierung von Drohnen-gestützter Logistik in München

Für das Beispiel werden zufällige Standorte innerhalb Münchens generiert. Jede Drohne kann maximal drei Gegenstände mitnehmen, wobei jeder Standort einen davon benötigt. Ziel ist es, alle Lieferungen so schnell wie möglich abzuwickeln (Minimierung der Zielfunktion, in diesem Fall die zurückgelegte Gesamtstrecke). Sobald die Drohne alle drei Gegenstände ausgeliefert hat, muss sie für die erneute Beladung zurück zum Lagerhaus.

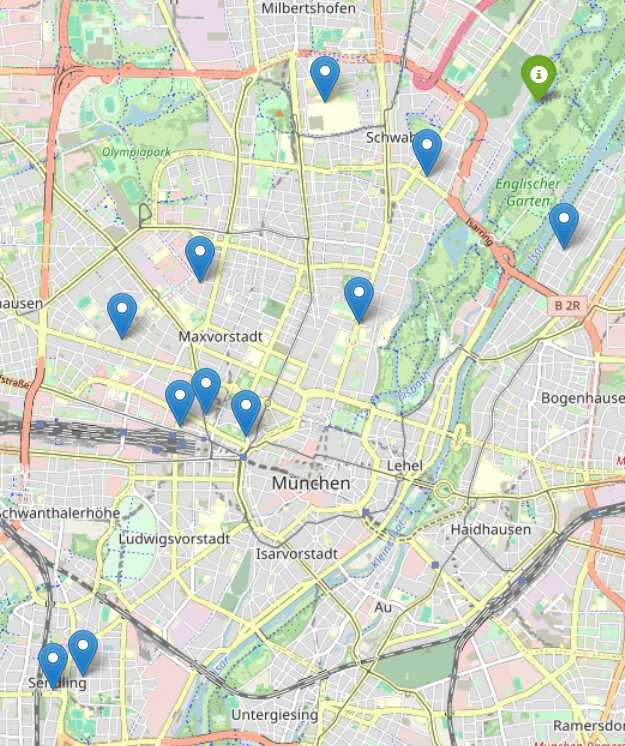
Es folgt die Definition der Nebenbedingungen und Einschränkungen:

• Erfüllung der Nachfrage an jedem Standort
• Kapazitätsgrenzen der Drohne dürfen nicht überschritten werden
• Keine doppelten Besuche innerhalb einer Tour
• Eliminierung von Subtouren und Umwegen

Das gesamte Modell wird an die HybridSolver-API übergeben, um die effizientesten Routen zu berechnen.

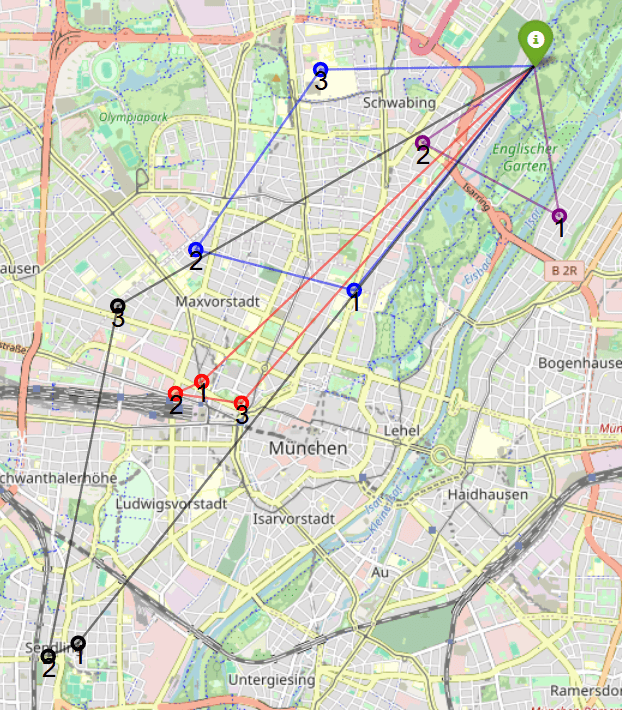
Die Lösung fasst ähnliche Orte in einem gemeinsamen Flug zusammen. Die Routenberechnung kann jedoch mit zunehmender Drohnenanzahl, variablen Nutzlasten und verschiedenen Lagerhäusern zunehmend komplex werden. Probier es aus. Hier ist die code-Implementierung des Tutorials.